Nonlinear isotropic/kinematic hardening model
- Philip Dai

- Mar 19, 2024
- 2 min read
Updated: Oct 22, 2024
In the most analyses, the plasticity model we used for offshore pipelines, only have the following lines:
*material, name=mat
*Density
7.85E-09
*Elastic
207000, 0.3
*Plastic, HARDENING=COMBINED, NUMBER BACKSTRESSES=10
420.481124, 0.000000
430.233308, 0.000007
439.990218, 0.000023
......
*expansion
1.170E-05
In this example, we have defined the kinematic hardening component by specifying half-cycle (test) data. The above line is equivalent to:
*PLASTIC, HARDENING=COMBINED, DATA TYPE=HALF CYCLE, NUMBER BACKSTRESSES=10
If limited test data are available, and can be based on the stress-strain data obtained from the first half cycle of a unidirectional tension or compression experiment. This approach is usually adequate when the simulation will involve only a few cycles of loading.
Other ways of defining the kinematic hardening component:
DATA TYPE=STABILIZED
or
DATA TYPE=PARAMETERS
When C and gama are zero, the model reduces to an isotropic hardening model.
When gama is zero, the linear Ziegler hardening law is recovered.
When test data are given as functions of temperature and/or field variables, it is recommended that a data check analysis be run first. During the data check run, ABAQUS will determine several pairs of material parameters (C, gama), where each pair will correspond to a given combination of temperature and/or field variables. Since ABAQUS requires the parameter to be a constant, the data check analysis will terminate with an error message if is not a constant. However, an appropriate constant value of may be determined from the information provided in the data file during the data check run. The values for the parameters and the constant can then be entered directly as described above.
NUMBER BACKSTRESSES
How many pairs of material parameters (C, gama) used in Abaqus internal fitting or calibration.
Outprint curve fitting information use card below:
*Preprint, echo=NO, model=YES, history=NO, contact=NO, parvalues=YES,PARSUBSTITUTION=yes
An example of curve fitting is shown below:
This example has shown that NUMBER BACKSTRESSES=4 achieved very good accuracy already. NUMBER BACKSTRESSES=3 is not bad either.
Strain hardening, also known as work hardening, is the strengthening of a metal or polymer by plastic deformation. This strengthening occurs because of dislocation movements and generation within the crystal structure of the material. Different hardening laws can be illustrated in the following graph.
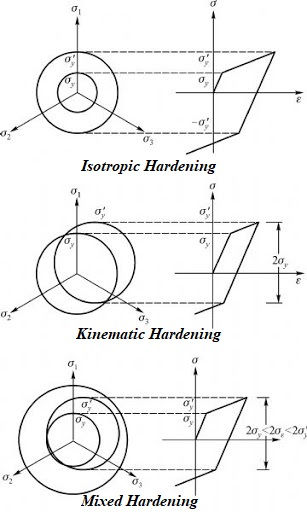
Defining the isotropic hardening component by the exponential law (not considered in our analyses).
Specify the material parameters of the exponential law Y0, Qinf, and b directly if they are already calibrated from test data. These parameters can be specified as functions of temperature and/or field variables.
Input File Usage:
*CYCLIC HARDENING, PARAMETERS
Some data from literature:
The following is extracted from the Abaqus theory manual:







Comments